
فرضیه صفر یا فرض صفر
فرضیه صفر یک مفهوم آماری است که تفاوت یا رابطه معنی داری بین متغیرهای اندازه گیری شده را نشان نمی دهد. این فرض، پیش فرض است مگر اینکه شواهد تجربی خلاف آن را ثابت کند.
فرضیه صفر بیان می کند که هیچ رابطه ای بین دو متغیر مورد مطالعه وجود ندارد (یعنی یک متغیر بر دیگری تأثیر نمی گذارد).
فرضیه صفر عبارتی است که یک محقق یا محقق می خواهد آن را رد کند.
آزمایش فرضیه صفر می تواند به شما بگوید که آیا نتایج شما به دلیل تأثیرات دستکاری متغیر وابسته است یا به دلیل شانس تصادفی.
چگونه یک فرضیه صفر را بنویسیم؟
فرضیههای صفر (H0) به عنوان سؤالات تحقیق شروع میشوند که محقق آنها را بهعنوان عباراتی بازنویسی میکند که نشاندهنده عدم تأثیر یا رابطه بین متغیرهای مستقل و وابسته است.
این یک حالت پیش فرض است که هدف تحقیق شما به چالش کشیدن یا تأیید آن است.
به عنوان مثال، اگر در حال مطالعه تأثیر ورزش بر کاهش وزن هستید، فرضیه صفر شما ممکن است این باشد: تفاوت معنی داری در کاهش وزن بین افرادی که روزانه ورزش می کنند و افرادی که ورزش نمی کنند وجود ندارد.
مثال های فرضیه صفر
| سوال تحقیق | فرضیه صفر |
| آیا نوجوانان بیشتر از بزرگسالان از تلفن همراه استفاده می کنند؟ | نوجوانان و بزرگسالان به همان میزان از تلفن همراه استفاده می کنند. |
| آیا گیاهان گوجه فرنگی در هنگام کاشت در کمپوست به جای خاک، سرعت رشد بیشتری را نشان می دهند؟ | بوته های گوجه فرنگی وقتی در کمپوست به جای خاک کاشته می شوند، تفاوتی در سرعت رشد نشان نمی دهند. |
| آیا مدیتیشن روزانه بروز افسردگی را کاهش می دهد؟ | مدیتیشن روزانه بروز افسردگی را کاهش نمی دهد. |
| آیا ورزش روزانه باعث افزایش عملکرد تست می شود؟ | هیچ رابطه ای بین زمان ورزش روزانه و عملکرد آزمون وجود ندارد. |
| آیا واکسن جدید از عفونت جلوگیری می کند؟ | واکسن بر میزان عفونت تأثیری ندارد. |
| آیا نخ دندان کشیدن روی تعداد حفره ها تأثیر می گذارد؟ | نخ دندان کشیدن روی تعداد حفره ها تاثیری ندارد. |
چه زمانی فرضیه صفر را رد می کنیم؟
ما فرضیه صفر را زمانی رد میکنیم که دادهها شواهد کافی قوی برای نتیجهگیری احتمال نادرست بودن آن ارائه میدهند. این اغلب زمانی اتفاق میافتد که مقدار p (احتمال مشاهده دادهها با ضمن درست بودن فرض صفر) کمتر از سطح معنیداری از پیش تعیینشده باشد.
اگر دادههای جمعآوریشده انتظارات فرضیه صفر را برآورده نکنند، محقق میتواند به این نتیجه برسد که دادهها فاقد شواهد کافی برای پشتیبانی از فرضیه صفر هستند و بنابراین فرضیه صفر رد میشود.
اما رد فرضیه صفر به این معنی است که بین مجموعه ای از متغیرها رابطه وجود دارد و اثر از نظر آماری معنی دار است (05/0p>).
اگر دادههای جمعآوریشده از نمونه تصادفی از نظر آماری معنادار نباشد، فرضیه صفر پذیرفته میشود و پژوهشگران میتوانند به این نتیجه برسند که بین متغیرها رابطه وجود ندارد.
شما باید یک آزمون آماری روی داده های خود انجام دهید تا میزان سازگاری آن ها با فرضیه صفر را ارزیابی کنید. p-value یکی از اندازه گیری های آماری است که برای تایید یک فرضیه در برابر داده های مشاهده شده استفاده می شود.
محاسبه p-value بخش مهمی از آزمون اهمیت فرضیه صفر است زیرا نشان میدهد که دادههای نمونه چقدر با فرضیه صفر در تضاد هستند.
سطح اهمیت آماری اغلب به صورت یک مقدار p بین 0 و 1 بیان می شود.
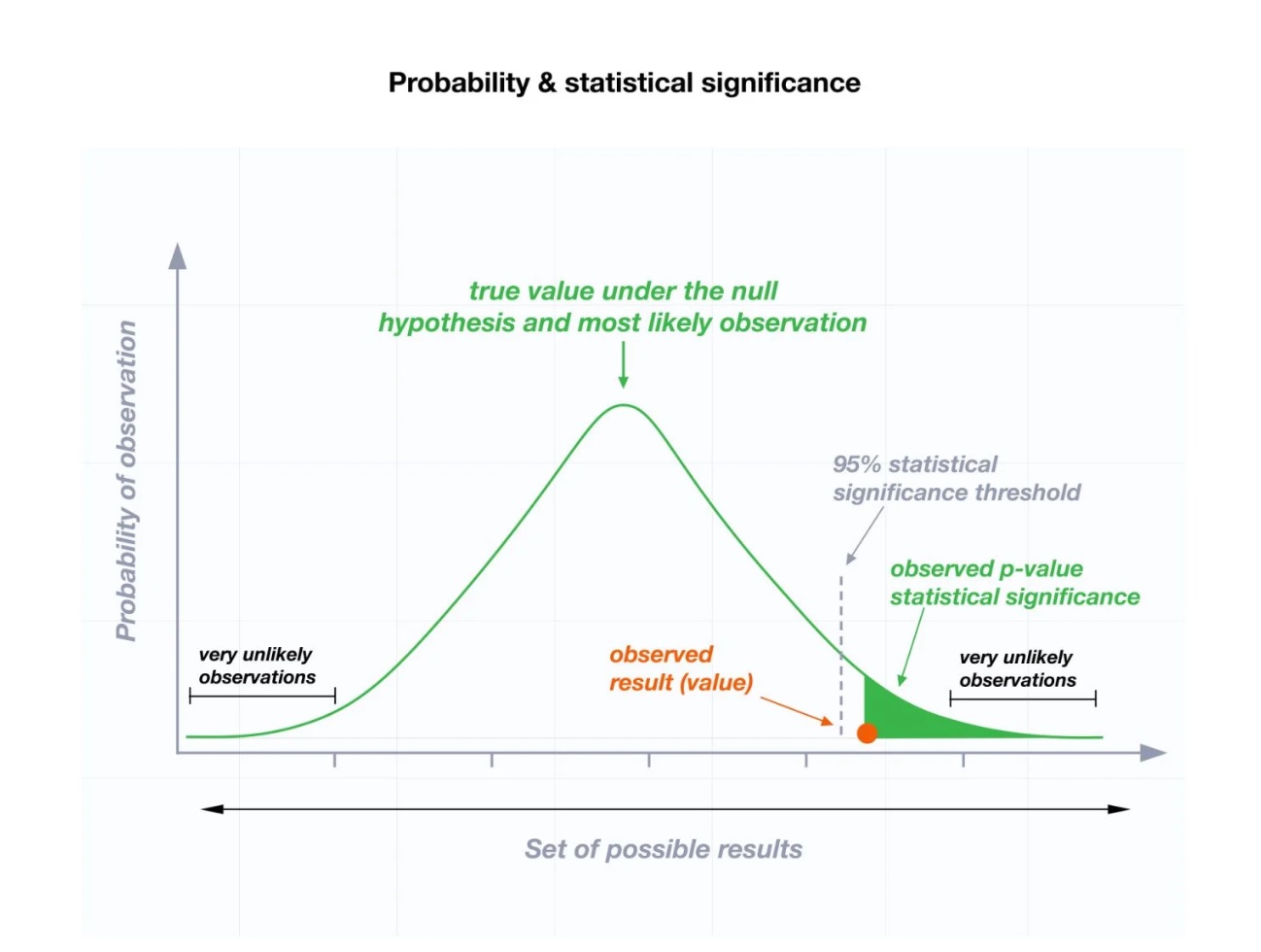
مقدار مشاهده شده از نظر آماری معنیدار است (p<=0.05)، بنابراین فرضیه صفر (N0) رد میشود و فرضیه جایگزین (Ha) پذیرفته میشود.
معمولاً یک محقق از سطح اطمینان 95٪ یا 99٪ (p-value 0.05 یا 0.01) به عنوان دستورالعمل های کلی استفاده می کند تا تصمیم بگیرد که آیا باید آن فرض صفر را رد کند یا حفظ کند.
هنگامی که مقدار p شما کمتر یا مساوی سطح اهمیت شما باشد، فرضیه صفر را رد می کنید.
به عبارت دیگر، مقادیر p کوچکتر به عنوان شواهد قوی تری در برابر فرضیه صفر در نظر گرفته می شوند. برعکس، وقتی مقدار p بیشتر از سطح معنیداری شما باشد، در رد فرضیه صفر شکست میخورید.
در این مورد، دادههای نمونه، دادههای ناکافی برای نتیجهگیری وجود اثر در جامعه فراهم میکند.
از آنجا که شما هرگز نمی توانید با اطمینان کامل بدانید که آیا تأثیری در جمعیت وجود دارد یا خیر، استنباط شما در مورد یک جمعیت گاهی اوقات نادرست خواهد بود.
هنگامی که شما به اشتباه فرضیه صفر را رد می کنید، به آن خطای نوع I می گویند. هنگامی که شما به اشتباه آن را رد نکنید، خطای نوع II نامیده می شود.
چرا ما هرگز فرضیه صفر را نمی پذیریم؟
دلیل اینکه نمی گوییم «صفر را قبول کن» این است که همیشه فرضیه صفر را درست فرض می کنیم و سپس مطالعه ای انجام می دهیم تا ببینیم آیا شواهدی علیه آن وجود دارد یا خیر. و حتی اگر شواهدی علیه آن پیدا نکنیم، یک فرضیه صفر پذیرفته نمی شود.
فقدان شواهد فقط به این معنی است که شما وجود چیزی را ثابت نکرده اید. اما ثابت نمی کند که چیزی وجود ندارد.
نتیجه گیری اینکه فرضیه صفر صرفاً به این دلیل که ما شواهدی برای رد آن پیدا نکردیم درست است، غلط و گمراه کننده است. همیشه این امکان وجود دارد که محققان در جاهای دیگر فرضیه صفر را رد کرده باشند، بنابراین ما نمیتوانیم آن را درست بپذیریم، اما در عوض، اظهار میکنیم که در رد فرضیه صفر شکست خوردهایم.
می توان فرضیه صفر را رد کرد یا در رد آن شکست خورد، اما هرگز نمی توان آن را قبول کرد.
چرا از فرضیه صفر استفاده می کنیم؟
ما هرگز نمی توانیم با قطعیت 100% ثابت کنیم که یک فرضیه درست است. ما فقط می توانیم شواهدی را جمع آوری کنیم که از یک نظریه حمایت می کند. با این حال، آزمایش یک فرضیه می تواند زمینه را برای رد یا پذیرش این فرضیه در سطح اطمینان مشخصی فراهم کند.
فرضیه صفر مفید است زیرا می تواند به ما بگوید که آیا نتایج مطالعه ما به دلیل شانس تصادفی است یا دستکاری یک متغیر (با سطح مشخصی از اطمینان).
اگر دادههای اندازهگیریشده بهطور قابلتوجهی بعید است که به وقوع پیوسته باشند، یعنی فرضیه صفر رد میشود و اگر نتیجه مشاهدهشده با موقعیتی که فرضیه صفر در اختیار دارد، سازگار باشد، فرضیه صفر پذیرفته میشود.
رد فرضیه صفر، زمینه را برای آزمایش های بیشتر فراهم می کند تا ببینیم آیا رابطه ای بین دو متغیر وجود دارد یا خیر.
آزمون فرضیه بخش مهمی از روش علمی است زیرا به تصمیم گیری در مورد اینکه آیا نتایج یک مطالعه تحقیقاتی از یک نظریه خاص در مورد یک جمعیت معین پشتیبانی می کند یا خیر کمک می کند. آزمون فرضیه روشی سیستماتیک برای پشتیبانی از پیشبینیهای محققان با تجزیه و تحلیل آماری است.
این به ارائه شواهد آماری کافی کمک می کند که فرضیه خاصی در مورد پارامتر جمعیت را یا به نفع یا رد کند.
هدف از یک فرضیه صفر
- هدف اصلی فرضیه صفر، رد یک فرض است.
- فرضیه صفر چه رد یا پذیرفته شود، می تواند به پیشرفت بیشتر یک نظریه در بسیاری از موارد علمی کمک کند.
- از یک فرضیه صفر می توان برای تعیین میزان سازگاری نتایج مطالعات متعدد استفاده کرد.
آیا همیشه به یک فرضیه صفر و هم به یک فرضیه جایگزین نیاز دارید؟
فرضیه صفر (H0) و جایگزین (Ha یا H1) دو ادعای رقابتی هستند که تأثیر متغیر مستقل را بر متغیر وابسته توصیف می کنند. آنها متقابلاً منحصر به فرد هستند، به این معنی که تنها یکی از دو فرضیه می تواند درست باشد.
در حالی که فرضیه صفر بیان می کند که هیچ اثری در جامعه وجود ندارد، یک فرضیه جایگزین بیان می کند که بین دو متغیر از نظر آماری معنادار وجود دارد.
هدف از آزمون فرضیه، استنتاج در مورد یک جامعه بر اساس نمونه است. برای انجام آزمون فرضیه، باید فرضیه تحقیق خود را به عنوان فرضیه صفر و جایگزین بیان کنید. هر دو فرضیه برای پوشش هر پیامد احتمالی مطالعه مورد نیاز هستند.
سوالات متداول
تفاوت بین فرضیه صفر و فرضیه جایگزین چیست؟
فرضیه جایگزین، مکمل فرضیه صفر است. فرضیه صفر بیان می کند که بین متغیرها هیچ اثر یا رابطه ای وجود ندارد، در حالی که فرضیه جایگزین ادعا می کند که یک اثر یا رابطه در جامعه وجود دارد.
این ادعایی است که انتظار دارید یا امیدوارید درست باشد. فرضیه صفر و فرضیه جایگزین همیشه متقابلاً ناسازگار هستند، به این معنی که در هر زمان فقط یکی می تواند صادق باشد.
برخی از مشکلات مربوط به فرضیه صفر چیست؟
یکی از مشکلات اصلی فرضیه صفر این است که محققان معمولاً فرض میکنند که پذیرش صفر، شکست آزمایش است. با این حال، پذیرش یا رد هر فرضیه یک نتیجه مثبت است. حتی اگر باطل رد نشود، محققان همچنان چیز جدیدی یاد خواهند گرفت.
چرا فرضیه صفر را نمی توان پذیرفت؟
ما می توانیم یک فرضیه صفر را رد کنیم یا نکنیم، اما هرگز آن را نمی پذیریم. اگر آزمایش شما نتوانست اثری را تشخیص دهد، این دلیلی بر عدم وجود اثر نیست. این فقط به این معنی است که نمونه شما شواهد کافی برای نتیجه گیری وجود ندارد.
ما نمیتوانیم یک فرضیه صفر را بپذیریم زیرا فقدان شواهد چیزی را که وجود ندارد ثابت نمیکند. در عوض، ما در رد آن شکست می خوریم.
عدم رد فرض صفر نشان می دهد که نمونه شواهد کافی برای نتیجه گیری وجود اثر ارائه نکرده است.
اگر مقدار p بزرگتر از سطح معنی داری باشد، در رد فرضیه صفر شکست می خورید.
آیا فرضیه صفر جهت دار است یا غیر جهت دار؟
آزمون فرضیه می تواند شامل یک فرضیه جهت دار جایگزین یا یک فرضیه جایگزین غیر جهت دار باشد. فرضیه جهت دار فرضیه ای است که دارای علامت کمتر از («<“) یا بزرگتر از («>») باشد.
یک فرضیه غیر جهت دار حاوی علامت مساوی نیست (“≠”). با این حال، یک فرضیه صفر نه جهت دار است و نه غیر جهت.
فرضیه صفر پیش بینی این است که هیچ تغییر، رابطه یا تفاوتی بین دو متغیر وجود نخواهد داشت.
فرضیه جهت دار یا فرضیه غیر جهت دار فرضیه های جایگزین فرضیه صفر در نظر گرفته می شود.





پاسخگوی سوالات و نظرات شما هستیم