
همبستگی یا correlation
همه چیز درباره همبستگی (Pearson, Kendall, Spearman)
در انتهای بخش مواد و روش های مقاله که از مسائل آماری در مقاله صحبت می کنیم، یکی از مهمترین تحلیلها، همبستگی است. همبستگی یعنی تحلیل دو متغیره ای که قدرت ارتباط بین دو متغیر و جهت رابطه بین آن ها را می سنجد. از نظر قدرت رابطه، مقدار ضریب همبستگی می تواند بین منفی 1 تا مثبت 1 باشد. کلا عدد 1 یعنی بالاترین درجه همبستگی بین دو متغیر. هر چقدر به سمت صفر نزدیکتر شویم، قدرت همبستگی هم کمتر می شود. جهت رابطه را هم علامت مثبت و منفی تعیین می کند. علامت مثبت یعنی هر دو متغیر با هم زیاد یا کم می شوند اما علامت منفی یعنی رابطه منفی که یعنی وقتی متغیر 1 بالا می رود، متغیر 2 پایین می رود. در آمار، معمولا 4 نوع همبستگی را می سنجیم: Pearson, Kendall rank, Spearman, Point-Biserial.
همبستگی r پیرسیون
همبستگی r پیرسون رایج ترین آماره همبستگی برای سنجش رابطه بین دو متغییری است که به صورت خطی با هم ارتباط دارند. مثلا در بازار سرمایه، اگر بخواهیم ببینیم چطور دو سهم با هم در ارتباط هستند، همبستگی r پیرسون برای سنجش درجه رابطه بین آن ها استفاده می شود. همبستگی point-biserial هم با فرمول همبستگی پیرسون انجام می شود با این استثنا که یکی از متغیرها دوحالته یا dichotomous است. همبستگی پیرسون را با فرمول زیر محاسبه می کنیم:
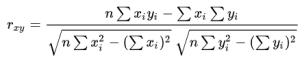
rxy = ضریب همبستگی r پیرسون بین x و y
n = تعداد مشاهدات
Xi = مقدار x (برای i مین مشاهده)
yi = مقدار y (برای i مین مشاهده)
انواع سوالات تحقیقی که همبستگی پیرسون می تواند بررسی کند:
آیا رابطه معناداری بین سن (بر حسب سال) و قد (اینچ) وجود دارد؟
آیا رابطه معناداری بین دما (سانتی گراد) و فروش بستنی (میزان درآمد) وجود دارد؟
آیا رابطه معناداری بین رضایت شغلی (JSS) و درآمد (ریال یا دلار) وجود دارد؟
فرضیات همبستگی پیرسون
برای همبستگی r پیرسون، هر دو متغیر باید توزیع نرمال داشته باشند. در ضمن خطی بودن و واریانس همسانی (homoscedasticity) دو فرض مهم دیگر هستند. خطی بودن یعنی فرض وجود یک رابطه خطی مستقیم بین هر یک از دو متغیر و homoscedasticity یعنی داده ها به صورت مساوی حول خط رگرسیون پخش شده اند.
انجام و تفسیر همبستگی پیرسون
اندازه اثر یا Effect Size: شاید برای ارزیابی ضریب همبستگی نیاز به استاندارد Cohen باشد تا قدرت رابطه یا اندازه اثر را تعیین کنیم. ضریب همبستگی بین 0.10 تا 0.29 یعنی رابطه ضعیف، بین 0.30 تا 0.49 یعنی رابطه متوسط، و بالای 0.50 یعنی رابطه قوی.
داده های پیوسته: داده ها باید بازه ای (interval) یا نسبتی (ratio) باشند. یعنی دارای ویژگی های بزرگی و بازه های برابر بین دو واحد مجاور باشند (یعنی مقادیر برابری از متغیر سنجید شده بین واحدهای مجاور وجود دارد). مثال: سن: افزایش سن از 21 سالگی به 22 سالگی همان مقدار افزایشی است که از 60 سالگی به 61 سالگی داریم.
همبستگی رتبه ای Kendall:
همبستگی رتبه ای Kendall نوعی آزمون غیرپارامتری است که قدرت وابستگی بین دو متغیر را می سنجد. اگر دو نمونه a و b را در نظر بگیریم به طوری که اندازه نمونه هر یک معادل n است، می دانیم که کل تعداد جفت شدگی با b برابر است با: n(n-1)/2. از فرمول زیر برای محاسبه همبستگی رتبه ای Kendall استفاده می کنیم:
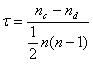
Nc= تعداد همخوان ها (یعنی با ترتیب مشابه)
Nd= تعداد ناهمخوان ها (یعنی با ترتیب متفاوت)
همبستگی رتبه ای اسپیرمن:
همبستگی رتبه ای اسپیرمن نوعی آزمون غیرپارامتری است که برای سنجش میزان رابطه بین دو متغیر استفاده می شود. نکته این جاست که همبستگی اسپیرمن فرضی را در رابطه با توزیع داده ها متصور نیست و تحلیل همبستگی مناسبی است وقتی که متغیرها روی مقیاسی سنجیده می شوند که حداقل ترتیبی (ordinal) است.
فرمول زیر برای محاسبه همبستگی رتبه ای اسپیرمن استفاده می شود:
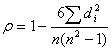
ρ: همبستگی رتبه ای اسپیرمن
di= تفاوت بین رتبه های متغیرهای متناظر
n= تعداد مشاهدات
انواع سوالات تحقیقی که همبستگی اسپیرمن می تواند پاسخ دهد:
آیا رابطه معناداری بین مدرک تحصیلی شرکت کنندگان (دبیرستان، لیسانس، فوق لیسانس و دکترا) و حقوق پایه شان وجود دارد؟
آیا رابطه معناداری بین موقعیت تمام کننده اسب در مسابقه و سن او وجود دارد؟
فرضیات همبستگی Spearman
فرض همبستگی اسپیرمن این است که داده ها حداقل ترتیبی باشند و نمرات یا امتیازات مربوط به یک متغیر باید به صورت monotonic با متغیر دیگر در ارتباط باشد. (یعنی لزوما ارتباط خطی ندارند اما جهت گیری ارتباط یکنواخت است)
اندازه اثر یا Effect Size: شاید برای ارزیابی ضریب همبستگی نیاز به استاندارد Cohen باشد تا قدرت رابطه یا اندازه اثر را تعیین کنیم. ضریب همبستگی بین 0.10 تا 0.29 یعنی رابطه ضعیف، بین 0.30 تا 0.49 یعنی رابطه متوسط، و بالای 0.50 یعنی رابطه قوی.
داده های ترتیبی: در مقیاس ترتیبی، سطوح متغیرها طوری مرتب شده اند که یک سطح را می توان بالاتر یا پایین تر از دیگری تصور کرد. اما اندازه تفاوت بین سطوح لزوما مشخص نیست. مثالش رتبه بندی سطوح تحصیلات است. فوق لیسانس از لیسانس بالاتر است و لیسانس هم از دبیرستان. اما نمی توانیم دقیق مشخص یا کمی سازی کنیم که فوق لیسانس چقدر از لیسانس بالاتر است. نمی توانیم هم بگوییم تفاوت بین فوق لیسانس و لیسانس معادل تفاوت بین لیسانس و دبیرستان است.





پاسخگوی سوالات و نظرات شما هستیم