آزمون کای دو یا مربع کای (Chi-square)
محققین علوم مختلف خصوصا زیست-پزشکی اغلب در بخش مواد و روش های مقاله شان با داده های اسمی یا دسته ای (Categorical) در تحلیل هایشان سروکار دارند (مثلا داده هایی که اکثرا به نولی لیبل دارند و نه مقدار عددی مثل نژاد، وضعیت استعمال دخانیات، و جنسیت). چون نمی توان داده های دسته ای را با استفاده از میانگین یا میانه خلاصه کرد، سنجش تمایل مرکزی (Central tendency) متغیرهای دسته ای با مد (Mode) انجام می شود. چون متغیرهای دسته ای صرفا می توانند یک سری مقدار مشخص داشته باشند، چنین داده هایی از توزیع نرمال پیروی نمی کنند. پس، نمی توان داده های دسته ای را با آزمون های رایجی مثل تحلیل واریانس (ANOVA)، یا همبستگی پیرسون و غیره تحلیل کرد. دلیلش این است که این آزمون ها نیاز به داده های پیوسته دارند. در عوض داده های دسته ای را می توانید اغلب با آزمون Chi-square تحلیل کنید.
انواع آزمون های Chi-square:
همان طور که در بالا گفتیم، آزمون Chi-square یا کای دو یا خی دو نوعی آزمون غیرپارامتری است که برای آزمودن فرضیه برای حالات متغیرهای دسته ای مورد استفاده قرار می گیرد. دو نوع آزمون کای دو که خیلی رایج هستند عبارتند از:
- آزمون کای دو برای تفاوت ها/استقلال:
این آزمون برای تعیین این مسئله استفاده می شود که آیا تفاوت یا رابطه آماری معناداری بین شمار (frequency) دو متغیر دسته ای یا طبقه ای یا رسته ای وجود دارد یا خیر. اگر برای بررسی رابطه باشد، بیشتر به آن آزمون کای دو استقلال گفته می شود.
مثال: تعیین اثر بالقوه داروی الف روی تب.
- آزمون کای دو نکوئی برازش (Goodness of Fit)
از آن برای تعیین این که آیا یک متغیر طبقه ای از یک توزیع فرضی تبعیت می کند یا خیر استفاده می کنیم. در واقع، از آن استفاده می کنیم تا ارزیابی کنیم که مدل ما چقدر خوب با داده های مشاهده شده همتراز یا fit است.
درجه آزادی در آزمون کای دو:
در آزمون کای دو، درجات آزادی یعنی تعداد اطلاعات مستقلی که برای محاسبه آماره کای دو استفاده می شوند. درجه آزادی برابر است با: df=(p-1)(q-1) که p تعداد ردیف های جدول و q تعداد ستون های جدول است.
مثال نحوه گزارش نتایج آزمون کای دو:
معمولا، آماره کای دو را همراه با تعداد نمونه (N) و درجه آزادی گزارش می کنیم. مثلا:
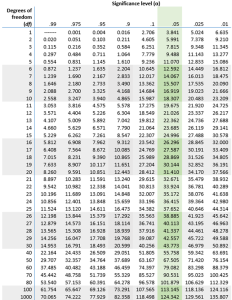
χ2 (1,N=84) = 8.9, p=0.003
عدد p=0.003 از محاسبه گر آمده است (https://www.socscistatistics.com/pvalues/chidistribution.aspx ).
حالا عدد 8.9 را با عدد متناظر جدول زیر (درجه آزادی بر حسب مقدار p) مقایسه می کنیم تا ببینیم ایا فرضیه رد می شود یا خیر. همان طور که می بینید عدد 8.9 از 6.635 (درجه آزادی 1 با p معادل 0.01) یا 3.841 (درجه آزادی 1 با p معادل 0.05) بزرگتر است، پس تفاوت معناداری وجود دارد با به ترتیب p=0.01 و p=0.05. یا به تعبیر دیگری p=0.003 هم از p=0.01 و هم از p=0.05 کوچکتر است پس فرض صفر رد می شود و تفاوت معناداری وجود دارد.
اندازه اثر در آزمون Chi-Square:
تا الان فهمیدیم ایا تفاوت معناداری وجود دارد یا خیر یعنی در واقع فرض صفر رد شد. حالا می خواهیم ببینیم قدرت رابطه بین دو متغیر چقدر است. این کار را با اندازه اثر یا Effect Size انجام می دهیم. در این جا از شاخص Cramér’s V برای تفسیر استفاده می کنیم. اگر این عدد 0.1 باشد، اثر کم و خفیف است، اگر 0.3 باشد متوسط است، و اگر هم 0.5 باشد یعنی اثر بزرگ است.
دقت کنید که طبق اصول، باید از χ یونانی و نه X انگلیسی استفاده کنید. برای این کار، از منوی insert در ورد، گزینه Symbol را زده و χ یونانی را در کنار سایر کاراکترهای یونانی پیدا کنید.





پاسخگوی سوالات و نظرات شما هستیم