آزمون نرمال بودن داده ها (Normality Test)
توضیح کامل آزمون نرمال بودن داده ها یا normality test: روش های ارزیابی نرمال بودن
آزمون نرمال بودن تعیین می کند که آیا داده های یک نمونه از یک جامعه با توزیع نرمال آمده استخراج شده یا خیر. این کار را معمولاً انجام می دهند تا تایید کنند آیا داده های موجود در تحقیق توزیع نرمال دارند یا خیر. رویه های آماری مختلفی مثل همبستگی، رگرسیون، تی تست، و ANOVA تحت عنوان آزمون های پارامتریک وجود دارند که بر اساس توزیع نرمال داده ها کار می کنند.
توزیع نرمال چیست؟
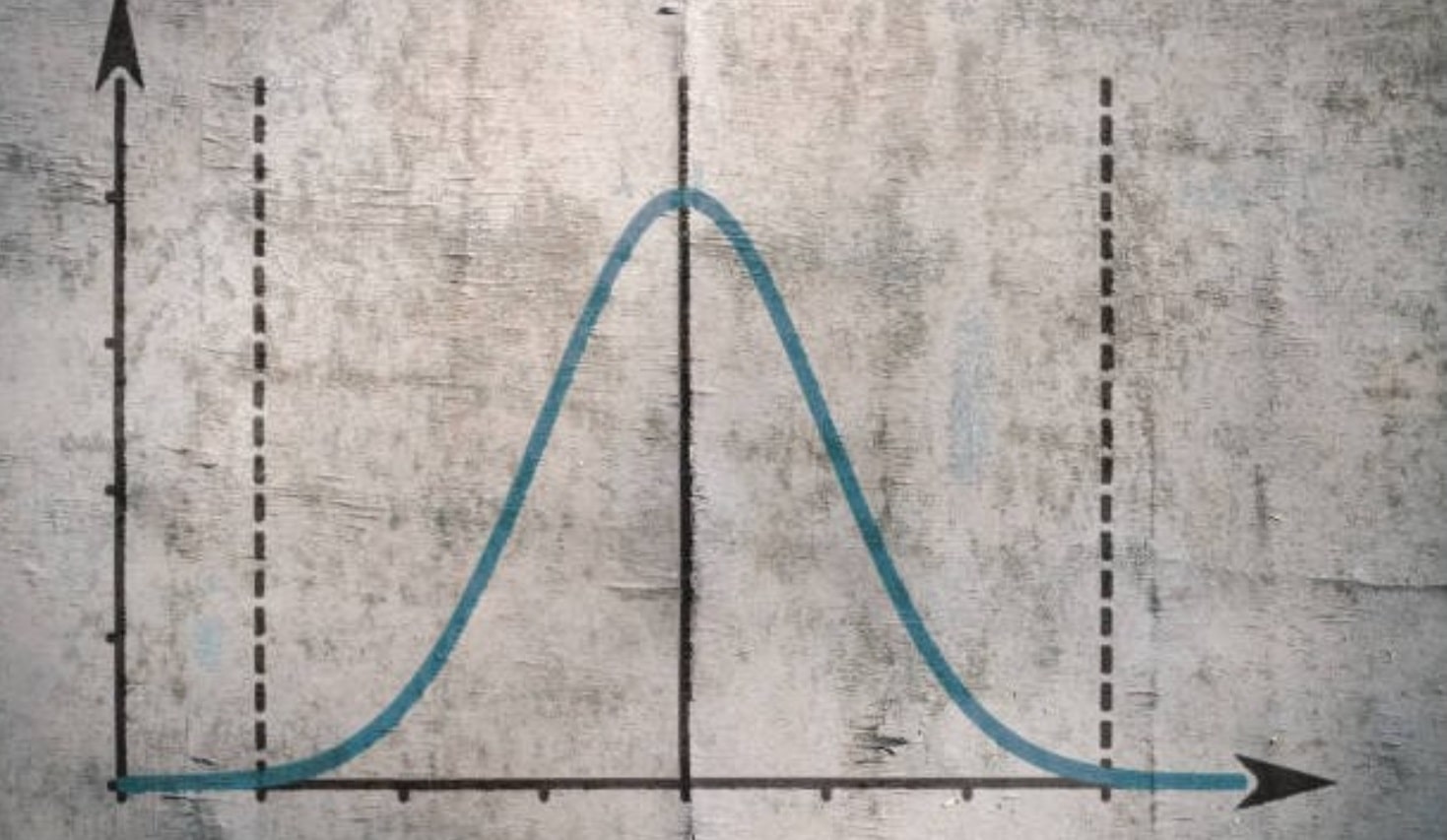
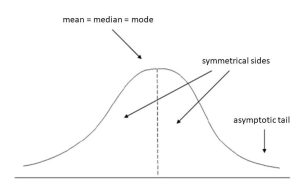
توزیع نرمال یا توزیع گاوسین مهم ترین توزیع احتمال آماری برای متغیرهای مستقل تصادفی است. اکثر محققین آن را تحت منحنی زنگوله مانند در گزارش های آماری می شناسند. توزیع نرمال برای متغیرهای پیوسته مناسب است. در واقع نوعی توزیع احتمال است که حول میانگین متقارن است یعنی سمت راست آینه سمت چپ است، که نشان می دهد داده های نزدیک میانگین بیشتر از داده های دورتر از آن اتفاق افتاده اند. سطح زیر منحنی توزیع نرمال مبین احتمال است و کل مساحت زیر نمودار جمعش به 1 می رسد. در یک توزیع کاملا نرمال، مقادیر میانگین، میانه و مد همگی یکسان هستند و قله نمودار را نشان می دهند.
روش های ارزیابی نرمال بودن
چند روش برای ارزیابی این که آیا داده های به طور نرمال توزیع شده اند وجود دارد و به طور کلی دو نوع هستند: 1) گرافیکال مثل هیستوگرام، نمودار احتمال Q-Q و 2) تحلیلی مثل آزمون های شاپیرو-ویلک و کولموگروف-اسمیرنوف.
روش های گرافیکی ارزیابی نرمال بودن داده ها
مفیدترین روش مصورسازی توزیع نرمال (یا نبود آن) برای یک متغیر مشخص رسم نموداری است که در ان داده ها به صورت توزیع فراوانی یا هیستوگرام رسم می شوند.
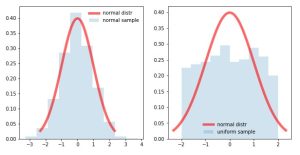
شکل: توزیع نرمال (چپ) در برابر غیرنرمال. منحنی قرمز رنگ مبین توزیع نرمال ایده آل (گاوسین) است.
توزیع نرمال شکل بالا برای توزیع نمونه واقعی (میله های خاکستری) کمی انحراف از منحنی توزیع نرمال نظری (خط قرمز) نشان می دهد. منظور این است که داده ها ما به طور نرمال توزیع شده ند. اما در توزیع غیرنرمال شکل بالا، نمونه از توزیع نرمال منحرف شده. روش های گرافیکی معمولا وقتی که اندازه نمونه کوچک است خیلی مناسب نیستند.
روش تحلیلی ارزیابی نرمال بودن
با پایه ای ترین فرآیند تحلیل داده شروع می کنیم. حین تحلیل داده، اطلاعات تجمیع شده (collated) از نقاط داده مختلفی به دست می آیند و برای همین مهم است تا چنین داده های تجمیعی را صادقانه ارائه دهیم یعنی به طوری که به بهترین شکل مجموعه داده را نمایندگی کند. داده های با توزیع نرمال با میانگین و انحراف از معیار به بهترین شکل و صادقانه ترین فرم ممکن تبیین می شوند. میانگین ریاضی مقداری است که از طریق جمع تمام مقادیر تقسیم بر تعداد مشاهدات به دست می آید، و انحراف از معیار هم شاخصی است برای پراکندگی متغیر (انحراف معیار کم یعنی پراکندگی کم یعنی تجمع حول میانگین و انحراف از معیار زیاد یعنی پراکندگی زیاد یعنی مقادیر اکثرا از میانگین دور هستند و به سمت دم نمودار پراکنده شده اند). در مقابل، مقادیری که به طور غیرنرمال توزیع شده اند خیلی با این دو شاخص خوب تبیین نمی شوند، بلکه بهتر است به کمک میانه و بازه های interquartile آن ها را تبیین نمود.
اولین قدمی که باید برداریم تا بررسی کنیم آیا توزیع متغیر از توزیع نرمال تبعیت می کند این است که آزمون نرمال بودن انجام دهیم، که معمولا می توان آن را با یک سری آزمون استانداردی که بخشی از اکثر نرم افزارهای آماری هستند انجام داد. مثال هایش عبارتند از کولموگروف-اسمیرنوف، شاپیرو ویلک، و داگوستینو-پیرسون. این آزمون ها داده ها را تحلیل می کنند تا ببینند آیا توزیعشان از توزیع نرمال به طرز معناداری انحراف پیدا می کند یا خیر (مثال: p-value). اگر p<0.05، توزیع به طرز معناداری از توزیع نرمال انحراف پیدا کرده.
از آزمون های پارامتریک زمانی استفاده می کنیم که توزیع تا حد خوبی از توزیع نرمال تبعیت می کند در غیر این صورت به سراغ آزمون های غیرپارامتری می رویم.
برای دو گروه داده، پرکاربردترین آزمون پارامتریک تی تست است (برای نمونه های مستقل یا زوجی، بر حسب داده هایمان)، و معادل غیرپارامتریک آن من-ویتنی است. برای بیش از دو گروه، آزمون پارامتری ANOVA و معادل غیرپارامتری آن کروسکال-والیس است.
برای همبستگی، آزمون پارامتریک مورد استفاده پیرسون بوده در حالی معادل غیرپارامتری آن اسیپیرمن است.
دقت داشته باشید که استفاده از آزمون اشتباه (مثلا پارامتری برای داده های بدون توزیع نرمال یا غیرپارامتری برای داده های با توزیع نرمال) می تواند به نتایجی کاملا غلط منجر شود. یعنی مثلا به اشتباه یافته های به طور آماری معنادار را غیرمعنادار یا یافته های غیرمعنادار را معنادار تبیین می کند.
به طور مشابه، وقتی تحلیل رگرسیون انجام می دهید، باید حواستان باشد که توزیع نرمال داده ها فرض مهمی برای انجام درست اکثر انواع تحلیل های رگرسیون است. یعنی نمی توان اکثر فرم های رگرسیون را با متغیرهای غیرنرمال توزیع شده انجام داد. شاید لازم باشد تا این متغیرها را به حالتی دیگر تبدیل کنیم (مثلا log-transformation، root-transformation و غیره) تا با اطمینان کافی به متغیری تبدیل شده با توزیع نرمال برسیم. این کار اغلب در تحلیل های آماری نادیده گرفته می شود و می تواند به یافته های غلط انگیز منجر شود.
امیدواریم که این مرور خلاصه و مفید اهمیت نرمال بودن توزیع متغیرها را به شما نشان داده باشد تا بدانید برای ارائه و مصورسازی داده ها طبق نرمال بودن، آزمون های نرمال بودن و معایب بالقوه هر کدام، بهترین گزینه را انتخاب کنید.





پاسخگوی سوالات و نظرات شما هستیم