آزمون کولموگروف- اسمیرنوف
آزمون کولموگروف- اسمیرنوف نوعی روش آماری است که برای ارزیابی شباهت بین دو توزیع احتمالی استفاده می شود. در واقع یک آزمون غیرپارامتریک است، به این معنی که هیچ فرضی در مورد توزیع داده ها ایجاد نمی کند.
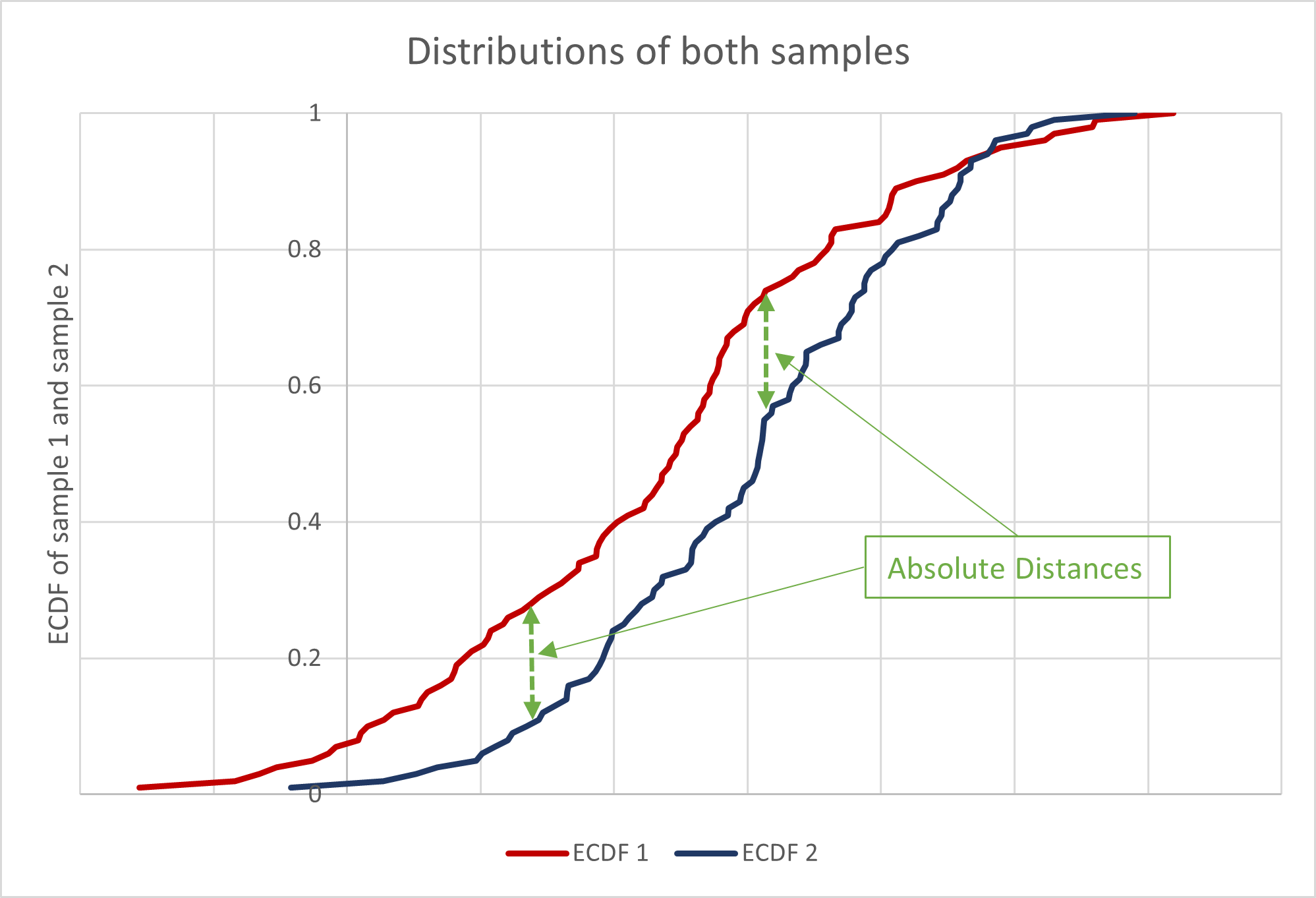
آزمون کولموگروف-اسمیرنوف مبتنی بر حداکثر تفاوت بین توابع توزیع تجمعی (CDF) دو توزیع مورد مقایسه است. آماره آزمون که به عنوان آماره D شناخته می شود، این تفاوت را اندازه گیری می کند و برای تعیین اینکه آیا این دو توزیع تفاوت معنی داری با یکدیگر دارند یا خیر استفاده می شود.
آزمون Kolmogorov-Smirnov طیف وسیعی از کاربردها را دارد: از مقایسه عملکرد دو مدل مختلف یادگیری ماشین گرفته تا تست نرمال بودن در یک مجموعه داده. همچنین معمولاً در آزمونهای برازش مناسب (Goodness-of-fit) استفاده میشود، یعنی برای مقایسه توزیع یک نمونه با توزیع نظری مورد استفاده قرار می گیرد.
تست KS به ویژه در کاربردهای علم داده مفید است زیرا می توان از آن برای مقایسه اثربخشی مدل های مختلف یادگیری ماشین استفاده کرد.
دانشمندان داده می توانند با مقایسه توزیع مقادیر پیش بینی شده از مدل های مختلف، بهترین مدل را برای یک کار مشخص شناسایی کنند.
انواع آزمون های کولموگروف اسمیرنوف
آزمون کولموگروف-اسمیرنوف چندین گونه دارد که هر کدام هدف متفاوتی دارند.
- تست تک نمونه ای
- تست دو نمونه ای
- تست تناسب برازش (Goodness-of-fit)
آزمون تک نمونه ای برای آزمایش اینکه آیا یک نمونه از یک توزیع خاص آمده است یا خیر استفاده می شود، در حالی که آزمون دو نمونه ای برای آزمایش اینکه آیا دو نمونه از یک توزیع یکسان آمده اند یا خیر استفاده می شود.
آزمون خوب بودن برازش برای آزمایش اینکه آیا نمونه از یک توزیع مشخص آمده یا یک توزیع نظری، استفاده می گردد.
مقدار بحرانی آماره آزمون از یک جدول به دست می آید یا با استفاده از فرمولی بر اساس حجم نمونه و سطح معنی داری انتخاب شده محاسبه می شود.
تست تک نمونه ای
آزمون KS تک نمونه ای برای آزمایش اینکه آیا نمونه از یک توزیع احتمال خاص می آید یا خیر استفاده می شود. فرض صفر این است که نمونه از توزیع مشخص شده آمده است.
آماره آزمون عبارتست از حداکثر اختلاف مطلق بین تابع توزیع تجربی نمونه و تابع توزیع تجمعی توزیع مشخص شده.
تست دو نمونه ای
آزمون KS دو نمونه ای برای آزمایش اینکه آیا دو نمونه از توزیع احتمال یکسانی می آیند یا خیر استفاده می شود. فرضیه صفر این است که دو نمونه از توزیع یکسانی می آیند.
آماره آزمون حداکثر اختلاف مطلق بین توابع توزیع تجربی دو نمونه است.
تست تناسب برازش (Goodness-of-Fit)
آزمون خوب بودن تناسب KS برای آزمایش اینکه آیا یک نمونه از یک توزیع مشخص آمده یا یک توزیع نظری استفاده می شود. فرض صفر این است که نمونه از توزیع مشخص شده آمده است.
آماره آزمون عبارتست از حداکثر اختلاف مطلق بین تابع توزیع تجربی نمونه و تابع توزیع تجمعی توزیع مشخص شده.
مزایا و محدودیت های آزمون کولموگروف-اسمیرنوف
آزمون KS به دلیل توانایی آن در مقایسه دو مجموعه داده و تعیین اینکه آیا آنها از یک توزیع گرفته شده اند یا خیر، شناخته شده است. همانند هر روش آماری، آزمون KS دارای مزایا و محدودیتهایی است.
آزمون کولموگروف- اسمیرنوف دارای چندین مزیت است که آن را به ابزاری مفید در تحلیل های آماری تبدیل می کند:
- غیرپارامتریک: آزمون کولموگروف-اسمیرنوف یک آزمون ناپارامتریک است، به این معنی که هیچ توزیع خاصی برای داده ها در نظر نمی گیرد. این آن را به یک تست همه کاره تبدیل می کند که می تواند در طیف گسترده ای از برنامه ها مورد استفاده قرار گیرد.
- پیاده سازی آسان: آزمون Kolmogorov-Smirnov به راحتی قابل پیاده سازی است و با استفاده از نرم افزارهای آماری ساده قابل انجام است. نیازی به دانش یا تخصص تخصصی ندارد.
- مناسب برای حجم نمونه کوچک: آزمون Kolmogorov-Smirnov را می توان با حجم نمونه های کوچک استفاده کرد و در شرایطی که داده ها محدود است مفید است.
با وجود مزایای آن، آزمون کولموگروف-اسمیرنوف محدودیت هایی نیز دارد:
- حساس به حجم نمونه: قدرت آزمون تحت تأثیر حجم نمونه است. با افزایش حجم نمونه، آزمون قدرتمندتر می شود.
- حساس به داده های پرت: آزمون به نقاط پرت در داده ها حساس است که می تواند منجر به رد نادرست فرضیه صفر شود.
- محدود به توزیع های پیوسته: آزمون کولموگروف-اسمیرنوف به توزیع های پیوسته محدود می شود و نمی توان از آن برای داده های گسسته یا مقوله ای استفاده کرد.
کاربردهای آزمون کولموگروف-اسمیرنوف
آزمون Kolmogorov-Smirnov (K-S) یک روش آماری همه کاره است که جایگاه خود را در زمینه های مختلف پیدا کرده است و قدرت خود را برای ارزیابی سازگاری بین توزیع های مختلف داده ها اثبات کرده است. ماهیت غیرپارامتریک و سازگاری آن به استفاده گسترده از آن در بخش های مختلف کمک کرده است.
- یادگیری ماشین:
تست K-S با اندازه گیری انحراف بین خروجی پیش بینی شده و نتایج واقعی به ارزیابی عملکرد مدل های یادگیری ماشین کمک می کند. این کمی سازی می تواند بینش های مهمی را در مورد رفتار مدل ارائه دهد.
با درک اینکه نتایج پیشبینیشده چقدر با نتایج واقعی همسو هستند، دانشمندان داده و مهندسان یادگیری ماشین میتوانند ترفندهای لازم را برای افزایش دقت و قابلیت اطمینان مدلهای خود انجام دهند.
- تجزیه و تحلیل آماری:
تست K-S با به ویژه هنگامی که با دادههایی مواجه میشویم که داده ها از منحنی زنگی مرسوم یا توزیع نرمال پیروی نمیکنند، مفید است. رویکرد غیرپارامتریک آزمون K-S ابزار قابل اعتمادی برای انجام چنین مقایسههایی فراهم میکند و به استنتاج نتایج معنادار از دادهها کمک میکند.
- تست های تناسب برازش:
تست K-S به عنوان یک تست عالی تناسب عمل می کند. محققان و تحلیلگران از آن برای تعیین اینکه آیا داده های نمونه آنها به توزیع فرضی پایبند است یا خیر، استفاده می کنند. چنین تعیینهایی در بخشهای مختلف بسیار مهم هستند، از امور مالی – جایی که درک توزیع برای مدیریت ریسک کلیدی است – تا زیستشناسی، جایی که الگوهای دادهها میتوانند بینشهایی را در مورد پدیدهها ارائه دهند، و مهندسی، جایی که سازگاری دادهها میتواند برای بهینهسازی فرآیند حیاتی باشد.
در تمام این کاربردها، آزمون کولموگروف-اسمیرنوف به دلیل سادگی و استحکام آن، نتایج قابل اعتمادی را بدون نیاز به فرضیات دقیق در مورد ماهیت داده ها ارائه می دهد.




پاسخگوی سوالات و نظرات شما هستیم