خطای نوع اول و خطای نوع دوم و آزمون فرضیه
نقطه شروع هر تحقیق: فرضیه یا مشاهده؟
اولین قدم در فرآیند علمی مشاهده نیست بلکه ایجاد یک فرضیه است که قابلیت آزمودن انتقادی را به کمک مشاهده و آزمایش دارد. از نظر پوپر، فیلسوف آلمانی، هدف یک محقق تایید نیست بلکه رد فرضیه اولیه است. منطقا غیرممکن است تا حقیقت یک قانون کلی را با مشاهدات زیاد بتوانیم تایید کنیم بلکه حداقل اصولا یک مشاهده می تواند برای نقض آن کافی باشد. مثلا، این که کلی قوی سفید ببینیم دلیلی بر اثبات این قضیه نیست که همه قو ها سفید هستند، بلکه مشاهده یک قوی سیاه برای رد این فرضیه کافی است.
ویژگی های یک فرضیه خوب
یک فرضیه خوب باید مبتنی بر یک سوال تحقیق خوب باشد یعنی باید ساده، مشخص و از پیش بیان شده باشد.
فرضیه باید ساده باشد:
یعنی یک متغیر پیشگو و یک متغیر خروجی یا پیامد داشته باشد مثلا سابقه مثبت اسکیزوفرنی در خانواده شانس ابتلا به این بیماری را در بستگان درجه 1 افزایش می دهد. این جا، متغیر پیشگو می شود سابقه خانوادگی اسکیزوفرنی و متغیر پیامد می شود خود اسکیزوفرنی در فرد. یک فرضیه پیچیده بیش از یک متغیر پیشگو یا یک متغیر پیامد دارد مثلا سابقه خانوادگی و وقایع استرس زای زندگی با افزایش شانس ابتلا به آلزایمر در ارتباط هستند. این جا دو متغیر پیشگو داریم: سابقه خانوادگی و وقایع استرس زای زندگی و فقط یک متغیر پیامد که می شود بیماری آلزایمر. یادتان باشد یک فرضیه پیچیده مثل این مورد را نمی توانیم با یک آزمون آماری منفرد تست کنیم و همیشه باید به دو یا چند فرضیه ساده شکسته بشود.
فرضیه باید مشخص و اختصاصی باشد
یعنی نباید جایی برای ابهام در رابطه با شرکت کنندکان و متغیرها، یا درباره این که چطور آزمون اهمیت آماری به کار گرفته خواهد شد بگذارد. در واقع از تعاریف عملیاتی ساده ای استفاده می کند که ماهیت و منبع شرکت کنندگان و همین طور رویکرد سنجش متغیرها را خلاصه می کند (سابقه دارودرمانی با آرام بخش ها، که بر اساس مرور پرونده پزشکی و نسخه های پزشک در سال گذشته سنجیده می شود، اغلب در بیمارانی که تلاش خودکشی داشته اند بیشتر از افراد کنترلی است که به خاطر دلایل دیگر در بیمارستان بستری شده اند). درست است که کمی این جمله ثقیل بود، اما در پروپوزال ها باید نوشته شود در حالی که شاید دقیقا در فرضیه تحقیق نیاید. به هر حال باید در ذهن محقق، وقتی که در حال مفهوم پردازی مطالعه هست، خیلی مشخص باشد.
فرضیه باید از پیش بیان شده باشد
یعنی باید در نوشتار حین بیان پروپوزال بیان شده باشد تا روی هدف اصلی تحقیق متمرکز باشیم و مبنای قوی تری برای تفسیر نتایج تحقیق در مقایسه یا فرضیه ای که در نتیجه وارسی داده ها ظاهر می شود، ایجاد کنیم. عادت آزمون فرضیه post hoc (که خیلی بین محققین رایج است) چیزی نیست به جز استفاده از روش های درجه سه روی داده ها (لایروبی یا dredging داده ها) تا حداقل به چیزی معنادار دست پیدا کنند. نتیجه اش می شود اغراق و بیخودی بزرگ جلوه دادن روابط شانسی در مطالعه.
انواع فرضیه
برای آزمودن اهمیت آماری، فرضیات بر اساس نحوه توصیف تفاوت مورد انتظار بین گروه های مطالعه، به دسته های مختلفی دسته بندی می شوند.
فرضیات null و جایگزین
فرضیه خنثی یا null می گوید که تفاوتی بین متغیرهای پیشگو و پیامد در جمعیت مد نظر ما وجود ندارد (تفاوتی بین عادات مصرف آرام بخش بیماران که تلاش خودکشی داشته اند با عادات بیماران کنترلی که از نظر سن و جنسیت مچ شده اند و برای بیماری های دیگری بستری شده اند وجود ندارد). فرضیه خنثی مبنای رسمی آزمودن اهمیت آماری است. با شروع این گفته که رابطه ای وجود ندارد، آزمون های آماری می توانند احتمال این که یک رابطه مشاهده شده به خاطر شانس و اتفاق بوده باشد را تخمین بزنند.
این گفته که رابطه ای وجود دارد – که بیماران با سابقه تلاش خودکشی عادات مصرف آرام بخش در آن ها از گروه کنترل متفاوت است – فرضیه جایگزین نامیده می شود. این فرضیه یا alternative hypothesis را نمی شود مستقیم اندازه گرفت؛ یعنی اگر ازمون اهمیت آماری فرضیه خنثی را رد کند، خود به خود خودش تایید می شود.
فرضیات جایگزین one and two-tailed
یک فرضیه one-tailed یا one-sided جهت رابطه بین متغیرهای پیشگو و پیامد را مشخص می کند. پیش بینی این که بیماران با سابقه خودکشی نرخ مصرف آرام بخش بالاتری نسبت به گروه کنترل دارند نوعی فرضیه یک طرفه است. اما دو طرفه می گوید صرفا نوعی رابطه وجود دارد و جهت آن مشخص نیست. یعنی مثلا در پیش بینی ما مشخص نیست بیماران خودکشی بیشتر آرام بخش مصرف می کنند یا کمتر. (منظور از tail یا دم همان نقاط انتهایی دم توزیع آماری مثلا منحنی نرمال زنگوله مانند است که برای آزمودن یک فرضیه استفاده می شود). فرضیه یک طرفه این مزیت آماری را دارد که امکان استفاده از یک اندازه نمونه کوچکتر را نسبت به موارد ممکن برای دو طرفه فراهم می کند. متاسفانه فرضیات یک طرفه همیشه مناسب نیستند در واقع برخی محققین معتقدند اصلا نباید از آن ها استفاده کرد. اما وقتی که صرفا یک جهت برای رابطه، مهم یا از نظر بالینی معنادار است مناسب هستند. مثالش می شود دارویی که نسبت به یک پلاسبو، تعداد بروز عوارض بیشتری دارد؛ یعنی احتمال این که دارو نسبت به پلاسبو عوارض کمتری داشته باشد ارزش تست کردن ندارد. به هر حال، از هر استراتژی ای که استفاده می کنید، باید از قبل آن را بیان کنید وگرنه دیگر قوت و انسجام آماری ندارد. لایروبی داده ها بعد از جمع آوری آن ها و حالت post hoc تصمیم راجع به تغییر برای آزمون فرضیه یک طرفه به منظور کاهش اندازه نمونه و P-value نشان دهنده نبود صداقت و درستی علمی (scientific integrity) است.
اصول آماری آزمون فرضیه یا تست فرضیه
یک فرضیه (مثلا چی چی هیدرامین با افزایش بروز یک سری تظاهرات روانی حاد در ارتباط است) در جهان واقعی یا درست است یا غلط. چون بررسی کننده نمی تواند تمام افرادی که ریسک این وضعیت را دارند را بررسی کند، باید این فرضیه را در نمونه ای از جمعیت هدف بیازماید. فارغ از این که محقق چقدر دیتا جمع می کند، هیچ وقت نمی تواند این فرضیه را به طور مطلق تایید یا رد کند. همیشه درباره پدیده های موجود در جمعیت از نظر اتفاقاتی که در نمونه می افتد مجبوریم استنباط انجام دهیم. به شکلی مشکل محقق شبیه به مشکل پیش روی یک قاضی است که می خواهد یک متهم را قضاوت کند (جدول 1). حقیقت محض که آیا متهم جرم را مرتکب شده را نمی شود تعیین کرد. به جایش، قاضی با فرض بیگناهی شروع می کند – یعنی متهم جرم را مرتکب نشده. قاضی باید تصمیم بگیرد آیا شواهد کافی برای رد فرضیه بیگناهی متهم وجود دارد یا خیر؛ این استانداردی است که شکی در اصولی بودن آن نیست. اما قاضی می تواند با متهم کردن یک بیگناه یا با عفو گناهکار واقعی اشتباه کند. به همین شکل، محقق با تصور فرض خنثی شروع می کند که یعنی رابطه ای بین متغیرهای پیشگو و پیامد در جمعیت وجود ندارد. بر اساس داده های جمع آوری شده در نمونه اش، محقق از آزمون های آماری استفاده می کند تا تعیین کند آیا شواهد کافی برای رد فرضیه خنثی به نفع فرضیه جایگزین (که رابطه ای در جمعیت وجود دارد) موجود هست یا خیر. استاندارد این آزمون ها به صورت سطح معناداری نشان داده می شود.
جدول 1: قیاس بین تصمیمات قاضی و آزمون های آماری
| قضاوت قاضی | آزمون آماری |
| بیگناهی: متهم جرم را مرتکب نشده | فرضیه خنثی: رابطه ای بین داروی فلان و تظاهرات روانی وجود ندارد. |
| جرم یا گناه: متهم جرم را مرتکب شده | فرضیه جایگزین: رابطه ای بین دارو فلان و تظاهرات روانی وجود دارد. |
| استاندارد لازم برای رد بیگناهی: فرای یک مقدار شک معقول | استاندارد برای رد فرضیه خنثی: سطح معناداری |
| قضاوت درست: محکوم شناختن مجرم | استنباط درست: نتیجه می گیرد که رابطه ای وجود دارد وقتی که واقعا در جمعیت وجود داشته باشد |
| قضاوت درست: تبرئه کردن متهم | استنباط درست: نتیجه می گیرد که رابطه ای وجود ندارد وقتی که واقعا در جمعیت وجود نداشته باشد |
| قضاوت اشتباه: محکوم شناختن متهم بیگناه | استنباط اشتباه (خطای نوع 1): نتیجه می گیرد که رابطه ای وجود دارد در حالی که در حقیقت وجود ندارد. |
| قضاوت اشتباه: تبرئه کردن متهم گناهکار | استنباط اشتباه (خطای نوع 2): نتیجه می گیرد که رابطه ای وجود ندارد در حالی که در حقیقت وجود دارد. |
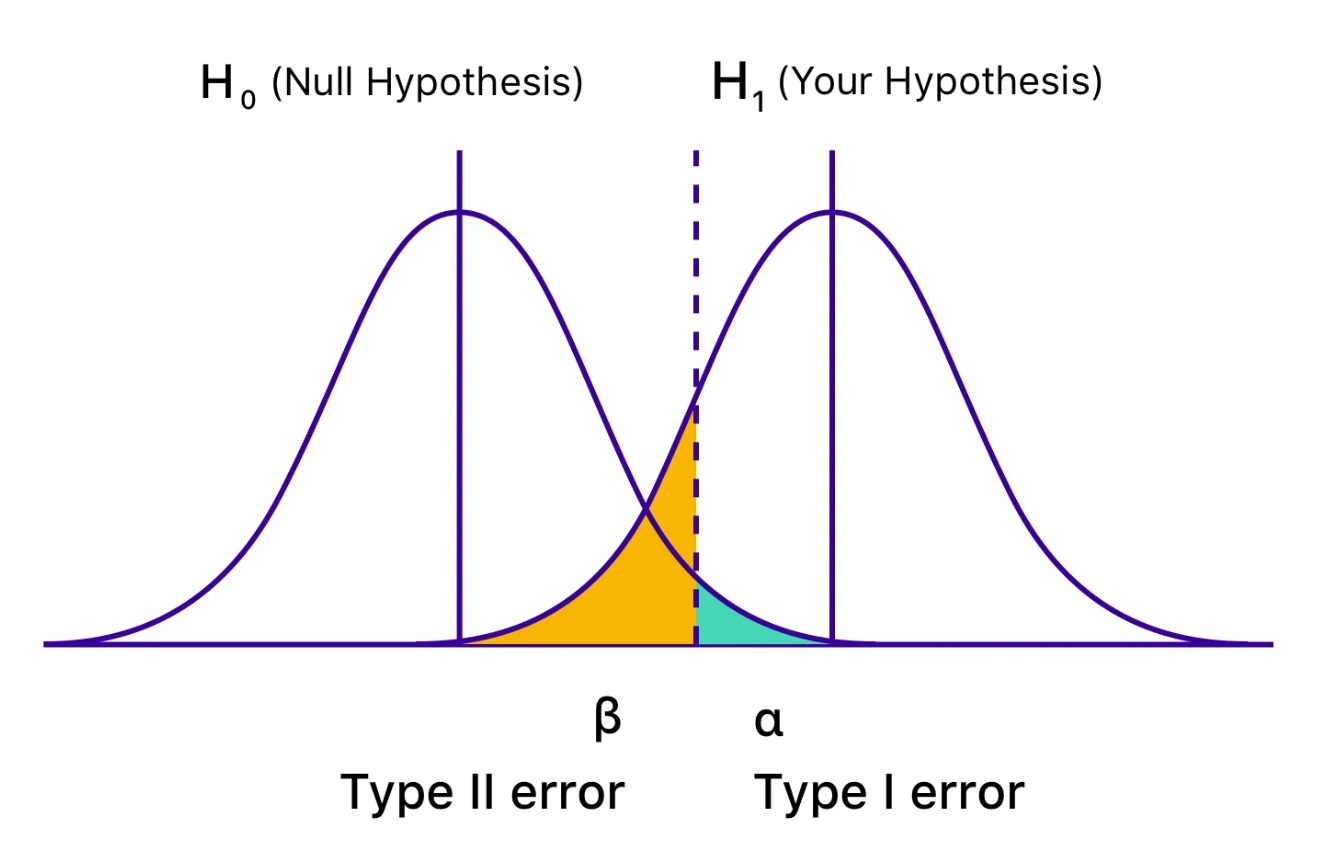
خطای نوع 1 (یا α) و خطای نوع 2 (یا β)
درست مثل نتیجه گیری یک قاضی، نتیجه گیری محقق شاید اشتباه باشد. گاها صرفا به خاطر شانس، نمونه معرف جمعیت مد نظر نیست. برای همین، نتایج موجود در نمونه واقعیت را در جمعیت منعکس نمی کند و اشتباه تصادفی به استنباط خطاآمیز منجر می شود. خطای نوع 1 (مثبت کاذب) زمانی اتفاق می افتد که محقق فرض خنثی ای را که حقیقتا در جمعیت خنثی بوده را رد کرده. حالا خطای نوع 2 (منفی کاذب) می شود وقتی که محقق فرض خنثی را رد نمی کند در حالی که این فرض خنثی در جمعیت اشتباه بوده. اگرچه از خطاهای نوع 1 و 2 نمی شود هیچ وقت کامل جلوگیری کرد اما محقق می تواند با افزایش حجم نمونه شانس آن را پایین بیاورد (هر چقدر که نمونه بزرگتر باشد، شانس اینی که تفاوت زیادی با جمعیت داشته باشد کاهش می یابد).
نتایج مثبت و منفی کاذب در اثر سوگیری هم می توانند اتفاق بیفتند (مشاهده گر، ابزار، یادآوری خاطرات و موارد مشابه و غیره) (البته دقت کنید خطاهای ناشی از سوگیری دیگر نوع 1 و 2 شناخته نمی شوند). این خطاها دردسر خاص خودشان را دارند چون شناسایی شان سخت بوده و به ندرت قابل کمی سازی هستند.
——————————
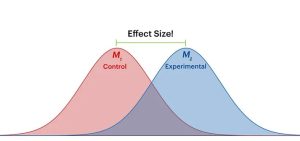
اندازه اثر
احتمال این که مطالعه ای بتواند رابطه ای بین یک متغیر پیشگو و یک متغیر پیامد را شناسایی کند صد البته بستگی به بزرگی حقیقی آن رابطه در جمعیت هدف دارد. اگر بزرگ باشد (مثلا 90 درصد افزایش در بروز تظاهرات روانی در افرادی که فلان دارو را مصرف می کنند)، شناسایی اش در نمونه آسان است. اما اگر اندازه رابطه کوچک باشد (مثل 2 درصد افزایش در تظاهرات روانی)، شناسایی اش در نمونه مشکل خواهد بود. متاسفانه، محقق اغلب بزرگی حقیقی رابطه را نمی داند – یکی از اهداف تحقیق تخمین آن است. به جایش، محقق باید اندازه رابطه ای که در نظر دارد در نمونه شناسایی کند را انتخاب کند. این اندازه یا مقدار را اندازه اثر یا effect size می گویند. انتخاب اندازه اثر مناسب سخت ترین جنبه برنامه ریزی مربوط به حجم نمونه است. گاها محقق از داده های مطالعات دیگر یا آزمون های پایلوت استفاده می کند تا حدس آگاهانه ای راجع به یک اندازه اثر معقول بزند. وقتی داده ای برای تخمین این موضوع وجود نداشت، محقق می تواند کوچکترین اندازه اثری که از لحاظ بالینی معنادار است را انتخاب کند مثلا 10 درصد افزایش در بروز تظاهرات روانی. البته که از نقطه نظر سلامت جامعه، حتی 1 درصد افزایش در بروز این موارد مهم خواهد بود. پس، انتخاب اندازه اثر همیشه کم و بیش قراردادی بوده و ملاحظات عملی را هم همیشه باید مد نظر داشت. وقتی که تعداد شرکت کنندگان موجود محدود باشد، محقق شاید مجبور شود عقب گرد حرکت کند تا تعیین کند آیا اندازه اثری که مطالعه اش قادر خواهد بود با X تعداد شرکت کننده شناسایی کند معقول خواهد بود یا خیر.
α، β و توان
پس از آن که مطالعه ای کامل شد، محقق از آزمون های آماری استفاده می کند تا سعی کند فرضیه خنثی را به نفع فرضیه جایگزین رد کند (خیلی شبیه به کاری است که یک وکیل انجام می دهد که سعی می کند قاضی را قانع کند تا بیگناهی را به نفع گناه و جرم رد کند). بر حسب این که آیا فرضیه خنثی در جمعیت هدف درست یا غلط است، و با فرض این که مطالعه سوگیری هم ندارد، چهار موقعیت ممکن است پیش بیاید (جدول 2). در دو مورد، یافته های موجود در نمونه و واقعیت موجود در جمعیت هدف با هم همخوانی دارند و استنباط محقق درست خواهد بود. اما در دو موقعیت دیگر، یا خطای نوع 1 (α) یا نوع 2 (β) اتفاق افتاده و استنباط غلط خواهد بود.
جدول 2: حقیقت در جمعیت در برابر نتایج به دست آمده از نمونه مطالعه: چهار حالت ممکن
| حقیقت در جمعیت | رابطه | نبود رابطه |
| رد فرض خنثی | درست | خطای نوع 1 |
| عدم رد فرضیه خنثی | خطای نوع 2 | درست |
محقق بالاترین شانس انجام خطای نوع 1 و 2 را در سیر تحقیق تجربه خواهد کرد. احتمال ارتکاب به خطای نوع 1 (رد فرضیه خنثی وقتی که واقعا خنثی است) را α می گویند یا اسم دیگرش سطح معناداری آماری است.
اگر مطالعه ای (داروی فلان و علائم روانی) با مثلا =0.05α طراحی شود آنگاه محقق ماکزیمم شانس به اشتباه رد کردن فرضیه خنثی را 5 درصد تنظیم کرده (و به اشتباه برداشت کرده که استفاده از فلان دارو و علائم روانی در جمعیت با هم ارتباط دارند). این همان سطح شک معقولی است که محقق حاضر است بپذیرد وقتی که از آزمون های آماری برای تحلیل داده ها پس از تکمیل مطالعه استفاده می کند.
احتمال ارتکاب خطای نوع 2 (عدم رد فرضیه خنثی وقتی که واقعا اشتباه است) β نام دارد. مقدار 1-β را توان می نامند یعنی احتمال مشاهده یک اثر در نمونه (if one) ی یک اندازه اثر مشخص یا بیشتر در جمعیت وجود دارد.
اگر β 0.10 فرض شود، محقق تصمیم گرفته که حاضر است 10 درصد شانس را برای از دست دادن رابطه ای با اندازه اثر مشخص بین فلان دارو و علائم روانی بپذیرد. این یعنی توان 0.90 بوده که یعنی 90 درصد شانس پیدا کردن رابطه ای با آن اندازه. مثال: فرض کنید که واقعا 30 درصد افزایش در بروز علائم روانی اتفاق خواهد افتاد اگر کل جمعیت فلان دارو را مصرف کنند. آن گاه، 90 دفعه از 100 دفعه محقق اثری معادل آن اندازه یا بیشتر در مطالعه خواهد دید. البته به این معنی نیست که محقق کلا نخواهد توانست اثر کوچکتری را شناسایی کند بلکه صرفا کمتر از 90 درصد شانس این اتفاق وجود دارد.
به طور ایده آل، خطاهای آلفا و بتا را صفر قرار می دهند تا شانس نتایج کاذب مثبت و منفی از بین برود. اما در عمل تا جای ممکن کوچک در می آیند. البته که کاهش آن ها معمولا مستلزم افزایش اندازه نمونه است. برنامه ریزی حجم نمونه تلاش می کند تا تعداد کافی شرکت کننده انتخاب کند تا مقادیر آلفا و بتا را تا جای ممکن پایین نگه دارد بدون آن که مطالعه بی خوردی گران یا مشکل شود.
خیلی مطالعات آلفا را 0.05 و بتا را 0.20 (میزان توان 0.80) قرار می دهند. این ها کم و بیش قراردادی هستند و مقادیر دیگری هم استفاده می شود: رنج عرف آلفا بین 0.01 و 0.1 است و برای بتا بین 0.05 و 0.20. به طور کلی، محقق باید مقدار آلفای کمتری انتخاب کند وقتی که نوع سوال تحقیق پرهیز از خطای نوع 1 (مثبت کاذب) را واقعا می طلبد. همین طور مقدار بتا هم باید کم باشد وقتی که خصوصا عدم خطای نوع 2 مهم می شود.
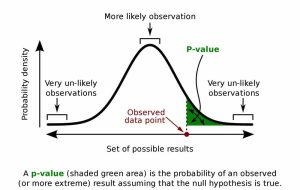
p-value
فرضیه خنثی مثل یک کیسه بکس عمل می کند: این فرضیه درست تصور می شود تا آن را به کمک یک آزمون آماری به یک فرض غلط شوت کنیم یا تبدیل کنیم. وقتی داده ها تحلیل شد، این آزمون ها p-value را تعیین می کنند یعنی احتمال این که با فرض درست بودن فرضیه خنثی، نتایج مطالعه شانسی به دست آمده. فرضیه خنثی به نفع فرضیه جایگزین رد خواهد شد اگر مقدار p کمتر از آلفا باشد یعنی سطح از پیش تعیین شده اهمیت آماری. نتایج غیرمعنادار – مواردی که p value از آلفا بزرگتر است مفهومش این نیست که رابطه ای در جمعیت وجود نداشته بلکه رابطه مشاهده شده در نمونه در مقایسه با موردی که صرفا می توانسته شانسی اتفاق افتاده باشد کوچکتر خواهد بود. مثلا، شاید محقق ببیند مردان با سابقه خانوادگی بیماری روانی دو برابر شانس بیشتری دارند که اسکیزوفرنی را نسبتا به افراد بدون این سابقه خانوادگی از خود بروز دهند، اما با مقدار p معادل 0.09. معنایش این است که اگر سابقه خانوادگی و اسکیزوفرنی در جمعیت با هم ارتباط نداشتند، 9 درصد شانس وجود داشت که چنین رابطه ای را به خاطر خطای تصادفی در نمونه پیدا کنیم. اگر محقق سطح معناداری را 0.05 ست کرده، باید نتیجه بگیرد که رابطه در نمونه از لحاظ آماری معنادار نبوده. شاید برای محقق وسوسه انگیز باشد تا نظرش را راجع به سطح معناداری پس از تحلیل عوض کند و بگوید نتایج به P<10 معنادار بوده. اما انتخاب بهتر این است که گزارش کند “اگرچه نتایج رابطه ای را نشان داد، اما به سطح معناداری نرسید (P=0.09)”. این راه حل اذعان می کند که اهمیت آماری یک موقعیت صفر و 100 نیست.
خلاصه دقت کنید که نمی توانیم هیچ چیزی را با آزمودن فرضیات و آزمون های آماری “اثبات” یا “رد” کنیم. بلکه فقط می توانیم فرضیه خنثی را رد کنیم و به طور پیش فرض فرضیه جایگزین را بپذیریم. اگر نتوانستیم فرضیه خنثی را رد کنیم آن گاه به طور پیش فرض آن را می پذیریم.



پاسخگوی سوالات و نظرات شما هستیم